From One Tomato Addict to Another

"My name is Kristina and I am a tomato addict!"

{unison reply} "HELLO KRISTINA"

Just to mix things up, today I give you a different sort of tomato addict. Meet the Tennessee Locavore. Some delicious recipes for your solanum lycopersicum. Enjoy!

METHINKS IT IS LIKE A WEASEL

Last night I read the post and comments over at Pandas Thumb about the latest kerfluff over a simple search algorithm given by Richard Dawkins in his 1986 book The Blind Watchmaker. "Oh That's Easy!" I thought, "It's so simple I could even code that in a spreadsheet."

This morning I did just that, and you can download the spreadsheet and try it yourself.

This being a spreadsheet a manual step is required, and some instructions are needed in any case. Below is a screen-shot of the spreadsheet:



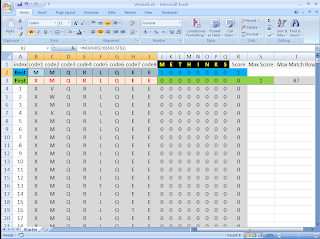
Columns B:I represent 8 letter codes that can be selected. Cells B3:I3 are the "parent" string, randomly generated letter A-Z, and below that are 500 "children" of the parent. Each letter has a 5% chance of being randomly replaced in each child string. (I'll come back to cells B2:I2).
Cells J1:Q1 (black block with yellow text) give a target string "METHINKS". Below this is a grade for the codes of the parent and each child string. Each of the 8 codes receive a 1 (one) if it matches the target, and a 0 (zero) if it does not. Theses grades are totaled to determine the "Score" for each. The maximum score is given, along with a row number of the maximum (used internally, it does not match actual row numbers).

For this first "generation" of children, the maximum number of matches to the target string is 1, and the codes corresponding to the first occurrence of this maximum, or the "best" scoring match, are displayed in cells B2:I2. The maximum Score is 1, and you can see that cell C2 contains the single correct match.

Now comes the manual step, because I don't want to get into macros for automatic updating:


1) Select cells B2:I2 and Copy.
2) Select cell B3.
3) Choose: Paste --> Paste Values. This should replace the contents of cells B3:I3 with what you copied from B2:I2.

The spreadsheet will automatically update (so fast you will probably miss it). Congratulations, you have just created generation #2. As you can see in my example above, the "best" string now has two correct matches. This manual step carries forward any improvement in matching the target string from one generation to the next.

Now repeat the manual step again for generation #3:


My example now has three correct matches. This would not have to be the case - it is possible to get a new generation where the score does not increase. It is even possible that the score among the children could actually go down; there is no latching. A score going down would be rare as I have defined this. I could increase the probability of this happening by increasing the mutation rate. Also, as I have defined this, the Score for the parent is included among the children's Scores, so the maximum Score cannot actually decrease from one generation to the next. That would be easy enough to change.

Generation #4:


Generation #5:


Generation #6:


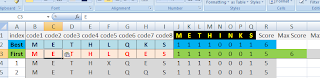
Generation #7:


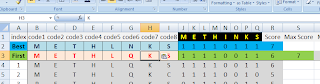
Generation #9:


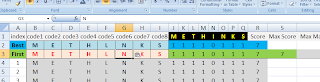
That's right, #9, not #8. My #8 did not improve in Score over #7, and so it stayed the same. In this case you can skip the cut-and-paste step and press the F9 key to recalculate the next generation instead.

Generation #10:


We have arrived! The Best string is now "METHINKS" which matches the target. No embedded information, just a crude sort of random hill-climbing algorithm.

Still this isn't a very good representation of evolution. An improvement representation would be to allow all the highest scoring children to reproduce, not just the first one as in my simple demonstration. I think perhaps Dawkins' original algorithm allowed for this.

I wonder what the folks over at Uncommon Decent will have to say about this?



Here is a link to some other WEASEL algorithms, originally organized by Ian Musgrave. I haven't actually looked at these, but I'll wager they are all better than mine.

When Zombies Attack!

TimesOnline has some important news for us :

The attached study, he said, highlighted "a problem we should wake up to -- this paper shows only the harshest control measures would give us a chance." Just what might this terrifying new threat be?

In my eagerness for a story, I hadn't noticed that Neil had added a smiley face at the end of his email. And when I opened the attachment, I discovered a paper entitled: "When Zombies Attack!: Mathematical Modelling of an Outbreak of Zombie Infection".

Move over swine flu. The zombies are coming...

[Image LaughingSquid]

Scary stuff, but even worse, the first commenter writes ...

I would just like to comment about the example of Zombies from '28 Days Later'.

They weren't actually Zombies; In the movie they are listed as the Infected. Zombies in the traditional sense cannot starve to death while the Infected in '28 Days Later' can in fact starve as seen in the ending scene.
[emphasis added]

[RantMode=ON]
This just kills me. There is no way in which the movie 28 Days Later does not completely satisfy all aspects of the zombie movie genre. A few seconds of emaciated, and more importantly [IIRC, 'cause ain't watching that dog again] partially dismembered ZOMBIES at the end does not make it not-a-zombie=movie.
[RantMode=OFF]
[Hat Tip to the Sciencepunk]

Lies, Damned Lies, and ... some more lies after that.

I just had this great idea for a blog titled "Lies, Damned Lies, and ____". So here is the main idea: a blog where every post is a lie. That's it. Very easy to write because I could just make it all up. No research needed! The inspiration for this was my discovery of the Sarah Palin page on Facebook. Aai-yai-yai, that could be a source of endless lampooning for the rest of my days. If that well runs dry, there is always Fox News.

Fortunately, I am time constrained by the projects I already have. Therefore I'll leave the idea open for any interested party.

[Update 9/06/2009]
It looks like someone may have taken me up on this. More likely they beat me to the punch. From Sun Dappled Forest:

That’s right. It is not just crazed flatulant loonies anymore. Even the right-wing is addressing the stories that are out there. It is being said that Glenn Beck raped and murdered a young girl in 1990.

Should I applaud, or cry?

[with a HatTip to Pull My Finger]

Monster of the Milky Way

Home for dinner, and Black Holes are on the menu. Time to try a little live blogging with NOVA on PBS.

David Brin describes black holes.

Space moving faster than light? I'm not familiar with that analogy. Space literally getting sucked up? Could they mean that space gets stretched or inflated instead?

Birth of a black hole.

Gregory Benford: "We think of black holes as God's dumpster, but they really are actors on the galactic stage."


Colliding galaxies, great fun.


More pretty pictures.



All in all, this program was big on pretty pictures and low on technical content, but then it appears to be intended for a younger audience, so maybe that is OK.

We still don't know what happens inside the black hole though, where the laws of physics break down. Mysteries await us.

Also ran: Reality

From The Pew Forum on Religion & Public Life:

When asked what they would do if scientists were to disprove a particular religious belief, nearly two-thirds (64%) of people say they would continue to hold to what their religion teaches rather than accept the contrary scientific finding, according to the results of an October 2006 Time magazine poll. Indeed, in a May 2007 Gallup poll, only 14% of those who say they do not believe in evolution cite lack of evidence as the main reason underpinning their views; more people cite their belief in Jesus (19%), God (16%) or religion generally (16%) as their reason for rejecting Darwin's theory.

Not so surprising really, people are generally afraid of change, of things they do not understand, and of letting go of the familiar. I might have to count myself in that group too.
[Hat Tip Improbable Research]

Death Panels Deflated

John Stewart's interview with Betsy McCaughey last week was eye opening, but I didn't really understand just what I was seeing until I watched the entire extended interview. In other words, "A lie can travel half way around the world in the time it takes truth to ties its shoes."

Most people don't have time to pay attention to the full story on anything - I surely don't, but if you are so inclined you can find links to all four parts of the interview below. If you are like most people and are in a hurry, maybe just skip to the last part about how Betsy McCaughey no longer has a job.

Betsy McCaughey on The Daily Show
Interview part 1 [With a Hat Tip to Greg Laden]
Interview part 2
Extended Interview part 1
Extended Interview part 2
... and the next day ...
Death panel originator Betsy McCaughey resigns in disgrace
[Image FreakingNews]

Mark CC is the Anti-Christ!

Another excellent critique from Mark CC The AntiChrist at Good Math, Bad Math.

Why The Public Option Sucks

[Via The Far Left Side, where you will find much more]

I Won! I Won!!

Such a contest it was too, since I floated the idea (see first comment) with the intent that creating something like this would be fun. My entry won out among the thousands of submissions and ... well ... maybe it was hundreds ... or at least a dozen ... ok ok, it was just me as far as I know, but I still had fun with it.

From misc

So perhaps I should explain what the heck I'm talking about? I should, but I'm really tired and have to get up very early in the morning, it is going to be short and abrupt:

A new blog - The Thomas Society - by Presbyterian minister Jonathan Weyer and friends, discuss rationality and religion, or maybe religious rationality, something like that (REALLY TIRED), needed an avatar for his blog award, "The Attie".

I'm very happy that Jonathan liked my image. I am happier still to read his blog, because it seems to provide the kind of rational discussion of religion I had given up on ever finding. Jonathan wins too, he's the latest addition to my Scientia Causidicus.

Giving rights to artificial intelligences

Author David Brin considers the issue of how Artificial Intelligences should be treated. A topic straight out of science fiction that really does deserve some attention before we actually have to deal with it.

The Real Reason to Ensure AI Rights

I've spoken elsewhere of one great irony -- that there is nothing new about this endeavor. That every human generation embarks upon a similar exercise -- creating new entities that start out less intelligent and virtually helpless, but gradually transform into beings that are stronger, more capable, and sometimes more brilliant than their parents can imagine.

The difference between this older style of parenthood and the New Creation is not only that we are attempting to do all of the design de novo, with very little help from nature or evolution, but also that the pace is speeding up. It may even accelerate, once semi-intelligent computers assist in fashioning new and better successors.

See the full article at Contrary Brin or Tomorrow Happens.

[Image Lifeboat.com]

Opposition to the Single Payer System

Environmental Roadie and Assistant Guitar Lawyer Sean Carman offers his views on health care reform domestic airport security. [Via The Huffington Post]

Why I Oppose the Single-Payer System
for Domestic Airport Security

Let me explain. There are any number of ways to ensure that passengers are prevented from bringing weapons or explosives onto domestic flights. Some advocate a "single-payer" system, in which a single entity, say, the United States government, becomes the sole source of funding for airport security. Under this plan, it would be the GOVERNMENT that organizes the provision of security services at all American airports.

That's right. GOVERNMENT employees would write the regulations dictating what items can be brought into the cabins of passenger aircraft. GOVERNMENT employees would operate the security checkpoints at America's airports. When someone walked through airport security, the person watching the metal detector to see if it registered an alarm to indicate the presence of metal in that person's pants would be a GOVERNMENT employee.

As you might begin to see, Sean isn't really talking about airport security at all. Go see what he is up to at The Huffington Post.

Posting Policy

It's nice to have visitors, but SPAM, not so much. I want to allow as much freedom for comments as I can, but there have to be some sort of limits too. Therefore, some rules:

1. Any posts or links which require any significant effort or my part to determine if they may or may not be legitimate or otherwise wastes my time are subject to immediate deletion.
2. If you want to promote your own blog*, do so by posting a relevant comment, or risk wasting my time (see rule #1). Promote yourself by participating.
3. No p@rn. No links to p@rn (see rule #1 again).
4. If you have a site with adult content that is not porn, and you are also legitimate visitor with something to say, then it would be polite to indicate your link is NSFW, Adult, etc.
5. If you must post in some language other than English, please give some indication of what language that is, or use an automatic translation service such as Google translate. I will not attempt to translated messages if there is no indication that it might be legitimate (see rule #1).
6. Be polite. Do not feed trolls. Do not be a troll.

* Good for you! I'd like to help. Now go back and finish reading the rule.

Please note that comments on posts more than 14 days old are subject to moderation, and will not appear immediately.

These rules are subject to my interpretation and may change at any time. If you think you have not been fairly treated, email me your concern and I will consider it.

More Health Care Reform Thoughts

The Daily Show With Jon Stewart	Mon - Thurs 11p / 10c
Glenn Beck's Operation
www.thedailyshow.com
Daily Show Full Episodes Political Humor Spinal Tap Performance

I had another thought, or maybe non-thought, on health care reform. See them at Nothing's Simple.

Sense on Health Care Reform

In the spirit of Mark Clifton's essay, I give you the Daily Show Panel on Health Care Reform:

The Daily Show With Jon Stewart	Mon - Thurs 11p / 10c
Healther Skelter - Obama Death Panel Debate
www.thedailyshow.com
Daily Show Full Episodes Political Humor Spinal Tap Performance

And there must be reform. Our current system, for all that it does well, is not sustainable, and is increasingly motivated by corporate profit. Among other things, the insurance industry has created a self-interested bureaucracy that is growing like a cancer.

Perhaps a disclaimer is in order: I an employed by a medical school, and arguably benefit when the health care industry make a good profit.

[Update]
My son asked me my opinion on health care reform after watching that Daily Show episode. And in explaining my views to him it occurred to me that medicine has a well established code of ethics, the first of which is "Do No Harm." Insurance coverage is increasing becoming a key part of health care, but the insurance industry is not bound by the same code of ethics. I think a successful reform should mandate that insurance companies operate within similar ethical guidelines.

[update: typo ... grrr]